Обзор темы

Обзор нашей темы 

"Движение тела, брошенного горизонтально или под углом к горизонту"

Теория

Движение тела, брошенного под углом к горизонту

Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения ; проекции ускорения на координатные оси равны а_х = 0, а_у = -g.

Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).

Проекции скорости тела, следовательно, изменяются со временем следующим образом:

,

где  – начальная скорость, α – угол бросания.

Координаты тела, следовательно, изменяются так:

При нашем выборе начала координат начальные координаты  (рис. 1) Тогда

(1)

Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета: 

.

(2)

Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.

Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t₀. Подставляя значение (2) в первую формулу (1), получаем:

.

(3)

Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.

Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем

.

(4)

Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:

и подставить его во второе уравнение. Тогда получим:

.

Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.

Теория

Движение тела, брошенного горизонтально

       

Движение тела, брошенного горизонтально,  можно  рассматривать как сложное, складывающееся из двух движений: равномерного  движения в горизонтальном направлении с начальной скоростью Vо и одновременного  свободного падения вниз.

Если с летящего самолета сбрасывается какой-то груз, то отделившись от самолета и падая вниз, этот груз одновременно продолжает совершать в воздухе движение в горизонтальном направлении.

Именно поэтому, когда сброшенный с самолета груз достигнет Земли, он будет находиться не над местом сброса, а далеко впереди него. Для прицельного сбрасывания груза летчику нужно учитывать и скорость самолета, и высоту, на которой он летит, и сопротивление воздуха, и, конечно, еще и скорость ветра.

Независимость свободного падения тела от его  движения  в горизонтальном направлении можно показать на опыте. Если на  краю подставки с отверстием поместить два одинаковых шарика, между которыми находится пластинка, удерживающая один из них над отверстием, то при ударе молоточка можно будет наблюдать свободное падение одного шарика и более сложное движение другого.

Эти два движения не только начинаются, но и заканчиваются одновременно. Специальные методы фотосъемки позволяют убедиться в том, что в любой момент времени эти шарики находились на одной и той же высоте.

Следовательно,  «появление»  горизонтальной скорости у одного из шариков никак не сказывается на  характере его движения в  вертикальном  направлении.  Шарик  просто "добавляет" к своему ускоренному движению по вертикали второе независимое движение по горизонтали. Происходит сложение двух независимых движений, в результате которого шарик движется неравномерно по криволинейной траектории.

На самом деле горизонтально брошенное тело не совершает двух отдельных движений - горизонтального и вертикального, оно просто движется по криволинейной траектории. При таком движении действие силы тяжести меняет величину и направление скорости. А мы используем этот несколько искусственный прием разделения движения на вертикальное и горизонтальное для упрощения наших рассуждений.

Если скорость  υ⃗ 0 направлена не вертикально, то движение тела будет криволинейным.

 

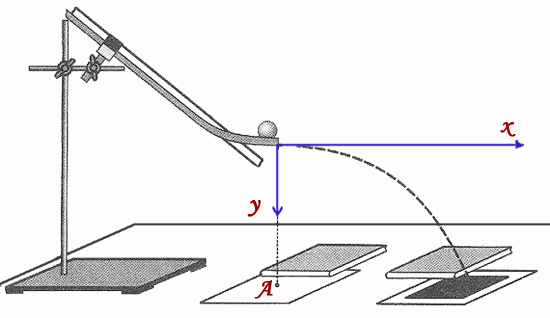
Рассмотрим движение тела, брошенного горизонтально с высоты h со скоростью  υ⃗ 0 (рис. 1). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ox и Oy. Начало отсчета координат совместим с начальным положением тела. Из рисунка 1 видно, что υ_0x = υ₀, υ_0y = 0, g_x = 0, g_y = g.

Тогда движение тела опишется уравнениями:

 υx=υ0, x=υ0t;(1)

 υy=gt, y=gt22.(2) υx=υ0, x=υ0t;(1)




 υy=gt, y=gt22.

Анализ этих формул показывает, что в горизонтальном направлении скорость тела остается неизменной, т. е. тело движется равномерно. В вертикальном направлении тело движется равноускоренно с ускорением  g⃗ , т. е. так же, как тело, свободно падающее без начальной скорости. Найдем уравнение траектории. Для этого из уравнения (1) найдем время   t=xυ0  и, подставив его значение в формулу (2), получим 

                                        y=g2υ 20x2

Это уравнение параболы. Следовательно, тело, брошенное горизонтально, движется по параболе. Скорость тела в любой момент времени направлена по касательной к параболе (см. рис. 1). Модуль скорости можно рассчитать по теореме Пифагора:

                                υ=υ  2x +υ  2y−−−−−−√  =υ  20 +(gt)2−−−−−−−−√.

Зная высоту h, с которой брошено тело, можно найти время t₁, через которое тело упадет на землю. В этот момент координата y равна высоте: y₁ = h. Из уравнения (2) находим

                                                     h=gt212

Отсюда

                                                              (3) t1=2hg−−√.

                                                            

Формула (3) определяет время полета тела. За это время тело пройдет в горизонтальном направлении расстояние l, которое называют дальностью полета и которое можно найти на основании формулы (1), учитывая, что l₁ = x. Следовательно,

l=υ02hg−−√   — дальность полета тела. 

v1=υ20+2gh−−−−−−−√. —   Модуль скорости тела в этот момент .